the triangle
Austin, TX
2011/07/17
A couple of years ago, I wrote a little program about triangles. The program calculates the area of a triangle given the base and the height. No great feat, right? Except, I did a little something special with the user interface. The triangle is graphed in a good old Cartesian coordinate system.† And, once the base of the triangle is set, you can “grab” the third vertex and move it around. All the while, the program keeps recalculating the area.
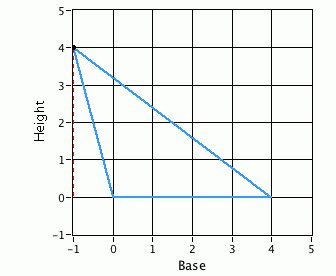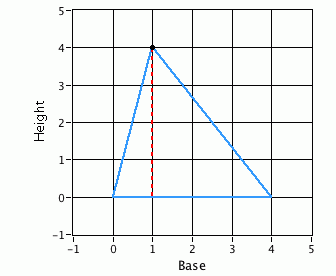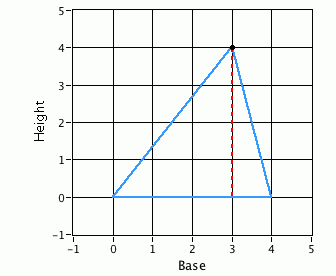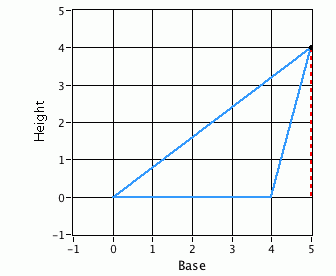
I asked a friend of mine, “If you grab that third point and just move it left or right, will the area of the triangle change?” What does your intuition tell you?
The triangles may look wildly different, but if the length of the base and height are set, the area is set as well. The animation on the right gives you a sense of this. Each triangle has an area of 8 units2.
This thing, about the area of different triangles being equal, is counter-intuitive, even for highly trained see-ers and thinkers. The triangles can look so different, but as long as they have the same base and height, the areas will be the same.
 Why are the areas the same? Because, the area of a triangle is the product of the length of the base, the height, and one-half. You can let all that make sense when you view a triangle as half of a parallelogram, or, even better, a rectangle. Take a look:
Why are the areas the same? Because, the area of a triangle is the product of the length of the base, the height, and one-half. You can let all that make sense when you view a triangle as half of a parallelogram, or, even better, a rectangle. Take a look:

 |
 |
 |
 |
 |
†↑ It was late in a small Bavarian town. It was the night between November 10th and 11th. You might imagine snow falling above the Danube. The year was 1619. Young René was merely 23, stationed in what is now southern Germany in the early days of the Thirty Years’ War. That night, René is said to have had three dreams altering the course of his life and ours.1
Nearly twenty years later, Descartes published his Discourse on the Method. The Discourse includes the oft quoted line, “Je pense, donc je suis.” Or, en anglais, “I think, therefore I am.” What is FAR more notable is the material contained in one of the appendices to the Discourse, La Géométrie.2 In this work, Descartes offers clear links between the formerly disjoint fields of Algebra and Geometry, laying important groundwork for the calculus.3
What about the Cartesian coordinate thingy? That is what brought you to this footnote. The Cartesian coordinate system is the “thing” Descartes employed/introduced/unleashed.4 It was to become the xy-graph we use, all too nonchalantly, to turn an equation into a graph.
The marriage Descartes performed on the fields of Algebra and Geometry gave us a brilliant new way to think about problems using both sides of our minds.5
1. (Yes, I just footnoted a footnote.) For a great description of these dreams and of the life and works of Descartes, pick up (and read) a copy of Amir Aczel’s Descartes’ Secret Notebook.
2. The MacTutor History of Mathematics archive is an excellent resource. The article on Descartes gives you all the basics and then some.
3. Calculus would arrive on the scene later in the same century, i.e. late 17th, with Newton and Leibniz in a mighty wrestling match for primacy. Wild coincidence of dates: Leibniz had a breakthrough on November 11, 1675 calculating the area enclosed by a curve and the x-axis of Descartes’ coordinate system. Yes, November 11. Fifty-six years after Descartes’ dreams, and eight days and 299 years before I was born.

4. The graphs in La Géométrie are not of the simple x–y style you saw in high school algebra. You can check it for yourself thanks to www.archive.org, and I popped one right there →
5. This “both sides of the brain” business is interesting to me. Certainly, different regions of the brain developed for different tasks. I don’t know about the whole left versus right deal. I have more to say about Algebra, Geometry, symbolic abstraction, and visualization in a comment on the Fibonacci post. Check it out if this footnote piqued your interest.


 The photographer for this post is Laurie Zimmerman Mann. Check out her site: www.lzmstudio.com.
The photographer for this post is Laurie Zimmerman Mann. Check out her site: www.lzmstudio.com.

6 thoughts on “Triangles”