Southeast Regional Library
Gilbert AZ
 The primes have gotten some good press this year. In January, a mathematician found a prime number with over 17 million digits.[2] He was participating in GIMPS, the Great Internet Mersenne Prime Search. Sort of like SETI, but these folks unleash the power of their personal computer on a search for large prime numbers. Yes, there is a search underway.
The primes have gotten some good press this year. In January, a mathematician found a prime number with over 17 million digits.[2] He was participating in GIMPS, the Great Internet Mersenne Prime Search. Sort of like SETI, but these folks unleash the power of their personal computer on a search for large prime numbers. Yes, there is a search underway.
As my seven-year old niece and I were chalking up some primes, we were sorting out which numbers to write based on whether or not you could add something (other than 1) repeatedly to get to it. For example, 4 is out since 2 + 2 = 4. 10? Nope, 5 + 5 = 10. When I asked her if we should include 21, we added our way up by 7s to see that 21 is not prime.
 You may recall a prime number is a number only divisible by 1 and itself, like 2. 2 is prime. The word “only” is the operative word in the definition. All numbers are divisible by one and themselves (trivial factors), but the primes have no other factors. Here are the first several primes:
You may recall a prime number is a number only divisible by 1 and itself, like 2. 2 is prime. The word “only” is the operative word in the definition. All numbers are divisible by one and themselves (trivial factors), but the primes have no other factors. Here are the first several primes:
2, 3, 5, 7, 11, 13, 17, 19, …
We humans have been thinking about prime numbers at least as far back as about 300 BC when Euclid included a proof about primes in his Elements.[3] About 100 years later, Eratosthenes[5] gave us a sieve for culling the primes. (MacTutor Prime numbers)
The University of Tennessee at Martin hosts a list of the first 1000 primes. How did UTM find those primes? With a sieve? Some other method? It can be hard to determine whether or not a number is prime. That is the point, the gift and the challenge of the primes.
Is 667 prime? Don’t look at the list, at least not yet. And, don’t Google it. First, see if you can sort it out with a pencil and some paper.
 Factoring big numbers is difficult, even for a computer. Internet encryption is the method by which your credit card number gets muddled up while in transit so evildoers can’t use it when they intercept it. (Yes, they do intercept. The game is to keep them from decoding what they catch.) This type of encryption is built on factoring numbers, which can be challenging especially when the number is a composite of two large prime numbers.
Factoring big numbers is difficult, even for a computer. Internet encryption is the method by which your credit card number gets muddled up while in transit so evildoers can’t use it when they intercept it. (Yes, they do intercept. The game is to keep them from decoding what they catch.) This type of encryption is built on factoring numbers, which can be challenging especially when the number is a composite of two large prime numbers.
Did you crack 667, yet? If so, try your hand at 8051. Compared to the numbers we use for encryption, these two numbers are not that big. Each of the prime factors of 667 and 8051 have fewer three digits.[7]
Now, imagine building a really big composite number by multiplying two primes each with thousands of digits. That giant of a number would take a computer a very long time to factor. That giant of a number could be a sort of lock. The key? One of the prime factors. You, with the help of your computer, keep one of the prime factors, and your credit card company keeps the other. While your 16 digit access to thousands of dollars of spending power is traveling over fiberoptic, it is protected by a giant number lock.[11]
 Okay, so we want big primes to make big numbers to send things privately. But, how do we find big primes? This is where Mersenne comes in. Mersenne was a French monk and contemporary of Fermat (think turn of the 17th century). He published a list of numbers, n, for which 2n − 1 is prime. Though his list wasn’t entirely correct, we named these creations Mersenne primes. Mersenne did good work as well as supported and encouraged the likes of Galileo, Descartes, and Huygens (without whom we wouldn’t even know what time it was). Mersenne earned the honor of being an eponym.
Okay, so we want big primes to make big numbers to send things privately. But, how do we find big primes? This is where Mersenne comes in. Mersenne was a French monk and contemporary of Fermat (think turn of the 17th century). He published a list of numbers, n, for which 2n − 1 is prime. Though his list wasn’t entirely correct, we named these creations Mersenne primes. Mersenne did good work as well as supported and encouraged the likes of Galileo, Descartes, and Huygens (without whom we wouldn’t even know what time it was). Mersenne earned the honor of being an eponym.
Let’s talk for a moment about the primeness of n in Mersenne’s 2n − 1. If 2n − 1 is prime, then n is prime. But, be careful with that if-then statement; the converse of the statement isn’t true.[13] (Run that by me again?) n being prime is a necessary condition for 2n − 1 to be prime, but it isn’t a sufficient condition. That is, n being prime won’t guarantee that 2n − 1 is also prime. We can check this out. Here are some Mersenne primes.
3, 7, and 31 are all prime and so are 2, 3, and 5. Let n = 11, another prime, and see what happens.
 But, 2047 = 23 * 89. It isn’t prime even though n is. So, our prime-hunting friends can use Mersenne’s 2n − 1 to get some good candidates, but then they have to confirm whether or not the candidate qualifies for primehood.
But, 2047 = 23 * 89. It isn’t prime even though n is. So, our prime-hunting friends can use Mersenne’s 2n − 1 to get some good candidates, but then they have to confirm whether or not the candidate qualifies for primehood.
Another question that tends to arise when people think about finding primes is whether or not there is some pattern to their distribution. This is and has been an enormous question for mathematics. The prime number theorem, proven in the late 1800’s, provides an approximation of the number of primes less than a given number, call it x. In a sense, the approximation gets better and better as x gets bigger and bigger, but the “better-ness” is relative to the size of numbers involved.[17]
The illustrious G.F.B. Riemann articulated a hypothesis about a relationship between the distribution of the primes and the zeros of something we math people have come to call the zeta function.[19] The Clay Mathematics Institute really wants you, or someone, to prove the Riemann hypothesis. In fact, they will give you one million US dollars if you do.
 Speaking of proofs, just this past May, a professor at the University of New Hampshire proved a theorem about the gaps between prime numbers. As the primes get larger, the gaps between consecutive primes seem to be growing.[23] Professor Zhang proved there are infinitely many pairs of consecutive primes that are not infinitely far apart. That is, the growing gap seems to have a cap for many, infinitely many, pairs of consecutive primes. This Slate article gives a good description of the problem. UNH has an article, too.
Speaking of proofs, just this past May, a professor at the University of New Hampshire proved a theorem about the gaps between prime numbers. As the primes get larger, the gaps between consecutive primes seem to be growing.[23] Professor Zhang proved there are infinitely many pairs of consecutive primes that are not infinitely far apart. That is, the growing gap seems to have a cap for many, infinitely many, pairs of consecutive primes. This Slate article gives a good description of the problem. UNH has an article, too.
One last prime note = About 887 words ago, I mentioned SETI. That wasn’t an accident. When I think of primes, I tend to think of the search for extraterrestrial life. I am not talking about an X-Files-style search through the low lands of New Mexico. (Though I have watched every episode about 2.414 times and saw many of them during primetime. (Yes, that happened.)) I am talking about the scientific efforts to investigate the reaches of space for other intelligent life. SETI’s early efforts in the 1960’s and 1970’s used radio telescopes to “beam” prime numbers into outer space.
Like I said, the primes get a lot of airtime.
My niece who helped with chalking some of those primes also insisted we decorate some of the chalk. When my brother-in-law asked if she had fun, she said, “Yes, it was awesome.” I agree.
2.↑ That is 17 million digits, not the value of the number. The value of the number is enormous, gargantuan, huge, unwieldy by everyday standards. The number one billion only uses 10 digits. According to the Daily Mail,
The number–2 to the power of 57,885,161 minus 1–is 17,425,170 numerals long and if you spent 12 hours a day writing it out at the rate of one digit a second it would take 403 days to complete.
Looking at this another way, you would need about 6000 sheets of paper (about 12 reams) to print out the new big prime. The someone who found this giant of a number is Dr. Curtis Cooper of the University of Central Missouri.
3.↑ In book IX Proposition 20, Euclid proves there are infinitely many primes. Sir Thomas Little Heath’s translation of Johan Ludvig Heiberg’s translation of Euclid has it stated thus: “Prime numbers are more than any assigned multitude of prime numbers.” Volume II of The Thirteen Books of Euclid’s Elements can be found for free in Google Play. I mentioned this is the same T.L. Heath in π. He also translated the work of Archimedes.
5.↑ Eratosthenes, a friend of Archimedes, was born in what is now Libya. He lived and worked in Alexandria and was one of the chief librarians there. Eratosthenes also is said to be the first to use the word “geography” albeit in Greek. (Wikipedia Eratosthenes)
7.↑ 667 and 9991 both have two and only two non-trivial divisors. The trivial divisors are 1 and the number. Here are the non-trivial ones: 23 * 29 = 667 and 83 * 97 = 8051. The non-trivial divisors for these two numbers are primes.
11.↑ Internet encryption is far more complicated than this. It involves modular arithmetic, a good night’s rest, and a steaming cup of coffee. The methods I am alluding to here are found in RSA, named for the three creators of this public-key encryption algorithm. Wikipedia’s RSA page provides more details.
13.↑ “If p, then q” does not imply “If q, then p.” A statement being true doesn’t guarantee the converse being true. Here is an silly example. If it is raining, the ground outside is wet. True-ish, you’ll agree. But, if the ground outside is wet, is it raining? I know you can argue particulars. So can I, but you get the point, yes? No, the point isn’t about how sprinklers also make the ground wet. The point is just because a statement is true, the converse may not be.
17.↑ The prime number theorem gives an asymptotic approximation for the number of primes less than a given value x. While the actual difference grows between the actual number of primes and the approximation x/ln(x), when you consider that difference in the context of the growing value of x, things are pretty good.
19.↑ The zeros of a function are those input values that when plugged into the function yield output values of 0. The zeros of f (x) = x2 − 9 are x = 3 and x = −3. More on Riemann’s zeta function soon.
23.↑ Twin primes are those cute little pairs like 3, 5 (or 5, 7; 11, 13; 17, 19; 29,31; …) that differ only by 2. The twin prime conjecture suggests, hopes, declares(?) there are infinitely many pairs of primes out there in the prime-osphere where both p and p + 2 are prime. Zhang’s proof may just move us closer to having proof in hand for the twin prime conjecture.


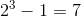
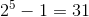
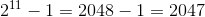












One thought on “Prime Parking”