Dallas TX
I grew up in the 1980s. Yes, yes. Duran Duran, leg warmers, MTV, Miami Vice, etc. (It was a special time.) Ronald Reagan was the U.S. President. We slowly but surely peeled our frosty selves out of the Cold War. Wealth was a central theme. Even as a youngster, I watched with interest as the walls of communism gave way to western capitalism. The pursuit of wealth was encouraged by quasi-laissez-faire policy makers, but one policy was not unmade.
It is not a policy as much as a rule, a formula, a computation. Compound interest, in all its glory, ruled the 80s as it has for centuries. At first glance, the formula for compound interest may seem complicated, but it arises naturally from the basic premises of savings and loans.
Now, I am not a banker, financial advisor, or Wall Street trader. I am sure there are subtleties beyond my knowledge: computation details in the bank’s software unbeknownst to me. Still, the formula here is the foundation for savings and loan computations. It arises naturally from the agreements we make when we say yes to compounding our interest.
Imagine it is 1980 and I am a forward-thinking six-year old. Instead of buying candy from the Keating Five and Dime[1], I save my birthday money and decide to put $100 in the bank. Mr. McDuck is offering to pay me 3% interest per year. In the simplest scenario, at the end of the year, he would pay me $100(0.03) = $3.00 in interest. (Remember 3% (“percent” means “per hundred”) = 3 hundredths = 0.03). So, I would have 100 + 100(0.03) dollars in the bank. Let’s simplify that expression using the distributive property.
100 + 100(0.03) = 100(1 + 0.03) = 100(1.03) = 103.00
No, no. Read it again. It isn’t that bad.
The situation is a little more complicated. Mr. McDuck is going to pay me the interest on a monthly basis. That is, he will pay 3% annually, compounded monthly. In all of his wisdom, he decides to divide the 3% APR (annual percentage rate) by 12 to determine the percentage to apply monthly. This way, at the end of the first month, Mr. McDuck pays me $100(0.03/12) = $0.25 in interest. So, at the end of the first month, I have $100(1 + 0.03/12) = $100.25 in the bank.
Mr. McDuck does not simply pay me twenty-five cents each month for 12 months. He compounds the interest. Each month, he is going to pay me interest on the principal (the $100 I deposited) and the interest he already paid me. At the end of the second month, he is going to multiply the balance in my account by (1 + 0.03/12).[2]
Mr. McDuck will likely round each month, but fractions of cents still make a difference.[3]
The pattern continues. At the end of the third month, I will have about $100.75 in the bank.
Notice the exponent is the number of months that have passed. To find the amount I have in the back after a year, I just need to put a 12 where the 3 was.[4]
That is $103.04 in the bank at the end of one year of compounding monthly. The more frequent compounding earned me an additional 4 cents. Big deal? Yes. That is four more cents than I had. For doing what? Leaving my money in McDuck’s (paws? webbed feat? articulated wings?).
How about after 10 years, you ask? It would be 1990, and I would be sitting in Algebra II with $134.94 in McDuck’s bank.
Twenty years? Well, after surviving the near insanity about Y2K, I would have $182.08.
The $82.08 earned in interest over 20 years may not seem like a big deal. EXCEPT, if I had put $10,000 in that same low-yield account, I would be sitting on $18,207.55.
Just like when it was a meager 100 bucks, I am nearly doubling my money over that 20 years.
Now, if the interest had been compounding only once per year, the balance after twenty years would only have been $18,061.11.
That is instead of the $18,207.55, a $146.44 difference in my favor.
Are you seeing the patterns? Compound interest makes money grow. The more frequent the compounding, the more money you make… or owe. Credit cards not only charge higher interest rates,[5] they compound the interest daily. Yes, daily. They don’t mess around.
You might also be noticing a formula.
where
A = amount after time t
P = principal (original amount)
r = annual interest rate as a decimal
n = number of interest payments per year
t = number of years
This formula works like a charm for a single amount left over time, but it would have been really forward-thinking of me to put money in the bank each month. Depositing $100 a month into McDuck’s 3% monthly account for twenty years would result in a savings account balance of about $32,912.28.[6] Not bad, considering my 240 $100 deposits amounted to $24,000. But, if I had it in an account offering 5%, the balance would have grown to $41,206.13. At 10%, there would be $76,126.73 in the bank in that same 20 years. Of course, I would have needed a source for that 100 bucks a month. At 6, I was devoting more time to watching Super Friends than building a revenue stream.
Now, maybe you wish you had a time machine. Then, you could go back to 1980 and start putting some money in the bank. Since time travel is not due to be released until the iPhone 88, invest in your future and put some money in the bank now. Twenty years will come.
1.↑ Yes, five and dimes were still around in 1980. My brothers and I bought plenty of Brach’s candy from a five and dime on Kalamazoo Avenue in Grand Rapids. Younger readers – Think 7-eleven run by your uncle or grandmother.
2.↑ Banks typically use average daily balance, not the balance at the end of the month. Since I am not depositing or withdrawing anything else, my balance is the same everyday and is the same as the average daily balance.
3.↑ The world is built on fractions of cents. Check with your local gas station, if you don’t believe me. Or, even more important, check with your credit card company. They love our fraction of sense.
4.↑ The exponent is the number of times the interest has been compounded. Monthly for one year is 12 interest payments per year.
5.↑ Depending on your credit score, you could be sitting on a card charging up to 30% APR. The national average is about 15%.
6.↑ The first deposit, after twenty years, would be
since 12*20 = 240. That is, the first deposit would have had interest compounded 240 times. The next deposit would have seen one fewer compounding. It was only cooking for 239 months.
This would continue all the way to the 240th deposit
which, as shown in the exponent, is only in the bank for one month. Then, the amount of money in the back after twenty years would be the sum of each deposit with its accumulated interest.
There is an easier way to compute the sum than brute force, i.e. doing 240 computations and then adding those 240 terms. You could use a spreadsheet. Or, there is a formula. We can find it.
The sum is a geometric series, a sum of a geometric sequence. Each term results from multiplying the previous term by a common value. For the above sum, the common multiplier is (1 + 0.03/12) = 1.0025.
Let’s just turn the series around a bit and call it S240.
We will apply a trick we used before. Multiply S240 by 1.0025.
Notice, the exponent on each term increased by one. Next, subtract 1.0025*S240 from S240. All of the terms will cancel except for the first term of S240 and the last term of 1.0025*S240.
Factor out the S240 on the left.
Solve for S240.
Factor out the $100 on the right to clear this up a bit.
This sum is approximately $32,912.28. There is a formula lurking in that equation for S240 and Sn in general. Do you see it?


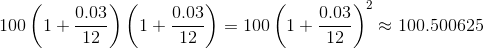
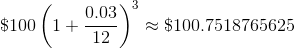
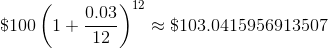
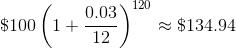
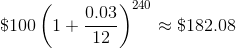
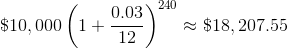
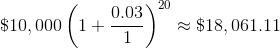
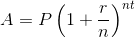






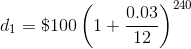
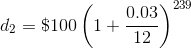
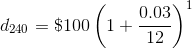
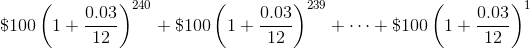
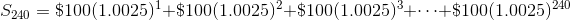
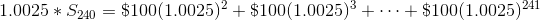
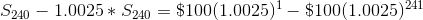
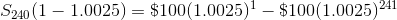
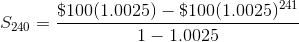
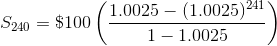
Dat’s a good one. Thanks, Eric!
>
Right on!
Thanks, Usserys!
Now, if we could only get the banker to compound continuously so that the rate of increase of our savings was directly proportional to the amount of savings we have in the bank – that would be exponentially cool ! But I suppose that would make the banker too busy making all those calculations. She wouldn’t have time for a cup of coffee !
Agreed!
Eric, Now this one I can follow all the way thru and it’s the example that I used in the RV business to demonstrate that leaving your compounding savings alone and financing your RV. Good job.
Thanks! If memory serves, I first learned about compound interest from you in your office at Fox’s.
fraction of sense. ha!
I couldn’t resist. That one was buried though. Thanks for reading!